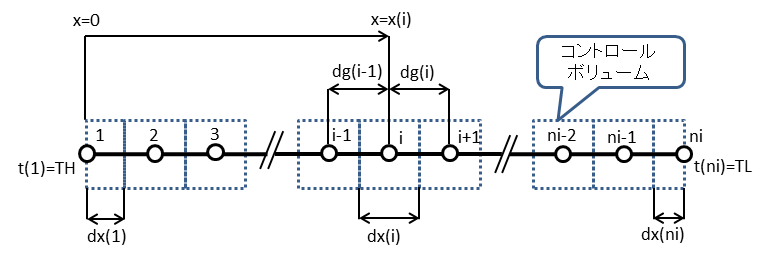
図1 格子点と距離の定義
Prof. Kazuhiro Fukuyo, Ph.D.
Yamaguchi University
Last updated: July 20th, 2011
【例題1】
温度TL = 300K (27℃)の大気中に長時間放置されていた厚さ0.2[m]の平板の一面を, 温度TH = 500[K]の熱源に接触させたとき,20[s]後の平板内の厚み方向の温度分布を求めよ。
ただし,熱源に接する面の温度は常にTHに等しいとする。また平板の熱伝導率λ,密度ρ, 比熱cはすべて一定とし,以下の値をとる。λ = 237.0[W/mK],ρ = 2688[kg/m^3],c = 905.0[J/(kg K)]。
(出典[1])
文献[1]では「陰解法」を使用しているが,ここではni個の格子点とコントロールボリュームを用いて 「陽解法」で計算する。
格子点と距離の定義を図1に示す。

格子点は温度を計算する点である。熱源に接する格子点の番号を1,大気側の格子点の番号をniとする。 格子点1と格子点niのそれぞれを包むコントロールボリュームの幅は通常のコントロールボリュームの半分程度なので, これらは通常「半コントロールボリューム」と呼ばれる[2]。
格子点の位置はx(1) = 0, ..., x(i), ..., x(ni)で定義される。 また,コントロールボリュームの幅はdx(1), ..., dx(i), ..., dx(ni)で定義される。 さらに格子点i-1と格子点iの距離はdg(i-1)で定義される。
先に格子点の位置を決定しておき,その後でコントロールボリュームの境界が 格子点同士のちょうど中間に来るように定義すると,x()とdx()とdg()の間の関係は次のようになる。
コントロールボリュームの幅や格子点の間隔は シミュレーションの分野ではしばしば「メッシュ間隔」とも呼ばれ, シミュレーションの空間分解能を表すために使われる。
1次元の熱伝導方程式は次の式で表される:
![]()
この式を格子点iについて「陽解法」で離散化すると次のようになる:
ここで,to(i)は現在の温度,t(i)は未来(dt時刻後)の温度を表す。 またalpha = αは温度伝導率で,α = λ / (ρ* c)である。
上式を整理すると次のようになる:
見やすくするために,ae(i) = alpha * dt / (dg(i) * dx(i)), aw(i) = alpha * dt / (dg(i-1) * dx(i))と置くと,上式は次のように書き直される:
上式を見て分かるように,to(i+1), to(i-1), to(i)の係数を合計すると1になる。 つまり,未来の温度t(i)は現在の温度to(i+1), to(i-1), to(i)の加重平均なのである。
陽解法による数値計算は極めてシンプルである。
初期条件to(1) = TH, to(2) = ... = to(i) = ... = to(ni) = TLに設定したうえで, i = 2〜ni-1について上の離散化方程式を適用すれば,dt時間後の温度 t(2), ..., t(ni-1)が求まる。
そしてさらにdt時間後の温度を予測したければ,to(2) = t(2), ..., to(ni-1) = t(ni-1) というように温度のデータを更新したうえで,改めて上の離散化方程式を適用して t(2), ..., t(ni-1)を算出すればよい。
すなわち,dt時間ずつ小刻みに計算を繰り返せば, 目的とする時間の温度分布が求められるわけである。
陽解法はシンプルで理解しやすいが,安定性の点で問題がある。to(i)の係数, (1 - ae(i) - aw(i))がマイナスの値になると,計算が不安定になる。 これを防ぐためにはdg(i), dx(i),すなわち空間分解能と dt,すなわち時間分解能をうまくバランスさせることが必要である。
必要なパラメータを入力し,計算を実施してみる。
結果は以下の通りである: