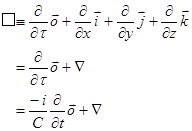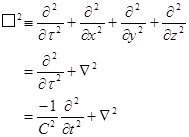相対論的熱伝導方程式の導出

解説：　福代和宏

(Updated: December 3, 2010)

1. 双曲型熱伝導方程式

従 来の放物型熱 伝導方程式の難点（温度情報伝達速度が無限大という問題）を克服するため，MorseとFeshbach [1], Cattaneo [2], Vernotte [3], Chester [4]らは双曲線型熱伝導方程式(Hyperbolic Heat Conduction Equation: HHCE)を提案した。

                                (1)

こ の式は熱バラ ンスの式：

                            (2)

と， 時間項を含 むフーリエの法則：

                          (3)

か ら導かれる 式：

                                 (4)

に おいてと定義することに よって得られる式である。Cは温度情報伝達速度である。

と ころで，温度 情報伝達速度が無限大であることはおかしいという考え方は相対論的立場から発せられたものである。いったい式(1)や式(3)は相対論 とどういう関係があるのだろうか？単に場当たり的(ad hoc)に作られた式に過ぎないのではなかろうか？

そ のような疑問 からスタートしたのが，AliとZhang [5]である。彼らは相対論の立場から熱伝導 方程式の構築に取り組んだ。

2. 相対論的時空間と演算子

時 間と空間を別 々に扱う古典力学の時空間と異なり，相対論の時空間（ミンコフスキー空間）では両者を等しく扱う。

時 間と空間の次 元をそろえるため，相対論では虚時間というものを導入する：

                                                        (5)

ま た時空座標をで表すことにする。

つ ぎに新しい演 算子，を導入する。これらは4次元の勾配，4次元のLaplacianともいうべきもので，それぞれ，quad, d’Alembertianと呼ばれる。

と 単位ベクトル を定義すれば，quadとd’Alembertianは次のように定義される：

        (6)

         (7)

3. 相対論的熱伝導方程式の導出

こ こで相対論的 熱伝導方程式(Relativistic Heat Conduction Equation: RHCE)を導出する。まず，従来の放物型熱 伝導方程式：

                                                  (8)

のをに置き換えて相対論的熱バランスの式を書くと，次の通りになる：

    (9)

こ れを整理する と，

                  (10)

と なり，式(1)に一致す る。

こ のように形式 的には相対論的熱伝導方程式(RHCE)と双曲線型熱伝導方程式(HHCE)の 間には違いが見られない。

し かし，丁寧に 導出過程を追うと，その違いがわかる。

ま ず，相対論的 立場では従来の熱バランスの式(2)が次のように書き換えられる：

                            (11)

ま た従来のフー リエの法則の式：

                                                                                 (12)

は 演算子の置き 換えで，次の式で表される：

                                                     (13)

式(13)を式(11)に代入 すると，式(10)が導出される。

つ まり，RHCEは従来 の熱バランスの式(2)とフーリエの法則(12)の相対論バージョンをベースにしているという点で，HHCEよりも 首尾一貫しているといえるのである。別の言い方で言えばエレガントであるといえる。

RHCEの熱力学的意義についてはまた稿を改めて紹介する。

参考文献 

[1] P. M. Morse, H. Feshbach, Method of Theoretical Physics, McGraw-Hill, New York, 1953

[2] C. R. Cattaneo: Sur une forme de l'équation de la chaleur éliminant le paradoxe d'une propagation instantanée, Compte. Rend. 247 (4) (1958), pp. 431 – 433

[3] P. Vernotte: Les paradoxes de la theorie continue de l'équation de la chaleur, Compte. Rend. 246 (22) (1958), pp. 3154 – 3155

[4] M. Chester: Second sound in solid, Phys. Rev. 131 (15) (1963), pp. 2013 – 2015

[5] Y. M. Ali, L. C. Zhang: Relativistic heat conduction, Int. J. Heat and Mass Transfer, 48 (2005), pp. 2397 – 2406