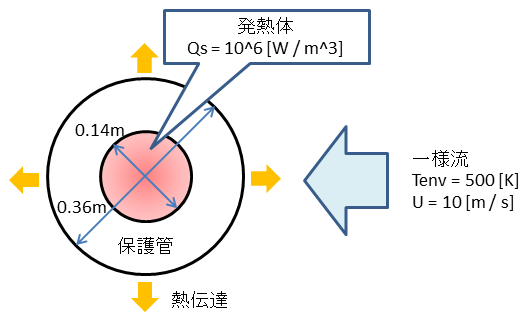
図1 発熱体と保護管の断面図
Prof. Kazuhiro Fukuyo, Ph.D.
Yamaguchi University
Last updated: July 21st, 2011
【例題2】
無限に長い外径0.36[m]，内径0.14[m]の保護管に直径0.14[m]の発熱体が同軸状に内蔵されている。
発熱体の熱発生率は10^6[W/m^3]，熱伝導率はλ1= 2.84 + 0.0105 T [W / m K]， 保護管の熱伝導率はλ2 = 102.8 - 0.0707 T [W / m K]とし，周囲には温度500 [K]， 流速10 [m / s]の高温空気が流れているものとする。
発熱体中心から保護管外表面までの半径方向温度分布を求めよ。
ただし，空気の熱伝導率，および動粘性係数は， それぞれλa = 7.24 × 10^3 + 6.36 × 10^-5 T [W / m K]， νa = -2.692 × 10^-6 + 1.368 × 10^-8 T [m^2 / s]であるとする。ただし，Tは温度[K]を表す。 (出典[1])
図1 発熱体と保護管の断面図
1次元の定常熱伝導問題である（だから比熱や密度のデータが入っていない） とはいってもこの問題には二つほど注意が必要な点がある：
文献[1]では定常の熱伝導方程式を離散化して， 温度分布や熱伝導率分布などが収束するまで繰り返し計算を行っているが， ここではわざと陽解法で非定常の計算を行い， 長い時間が経過したところを「定常状態」とみなして 温度分布や熱伝導率分布を求めることにする。 そのため，比熱や密度として仮の（適当な）値を与えて計算を行う。
格子点と距離の定義を図2に示す。 文献[1]とはコントロールボリュームの置き方が違うので要注意。
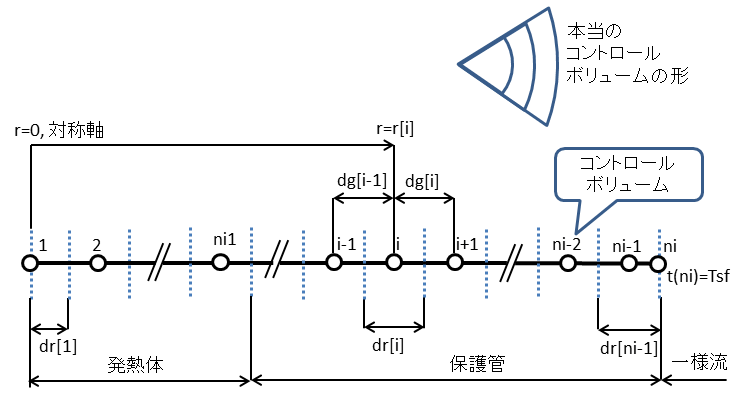
便宜上，図2ではコントロールボリュームの境界を平行の直線（点線）で描いているが， 実際には円筒形の空間に対するシミュレーションを行うので， コントロールボリュームの本当の形は右上にあるようなバウムクーヘンのかけら， もしくは円環のような形となる。
中心軸に位置する格子点の番号を1，空気に触れる表面の格子点の番号をniとする。 また，発熱体に属する格子点およびコントロールボリュームの番号を1〜ni1とする。
ここでコントロールボリュームに関して特殊な設定をしているのが，1とniの格子点である。 格子点1のまわりでは前回と同様に 半コントロールボリュームを設定している。 これに対し，格子点niのまわりにはコントロールボリュームを設けず， niの格子点をコントロールボリュームni-1の右側（東側）境界面に設定している。
今回の計算では格子点1とniの位置を
r[1] = 0, r[ni] = 0.18
と定義し，残りの格子点iの位置を
r[i] = 0.18 * (2 * i - 3) / (2* (ni - 2))
で定義する。
このように先に格子点の位置を決定しておき，その後でコントロールボリュームの境界が 格子点同士のちょうど中間に来るように定義すると，rとdrとdgの間の関係は次のようになる （格子点niのまわりだけ取り扱い注意）。
極座標で表した1次元熱伝導方程式は次のようになる（文献[2]）：
......(1)
ここで，θは温度[K]，rは管の中心からの距離（半径）[m]，tは時間[s]， Qは内部発熱量[W / m^3]である。 また，密度ρ，比熱c，熱伝導率λは場所によって異なる値をとるものと考えている。
コントロールボリューム法（なおかつ陽解法）でこの式を離散化することにする。 まず，式(1)の両辺にrをかける：
......(2)
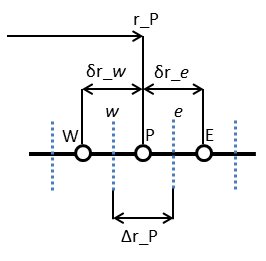
図3 コントロールボリュームP
つぎに図3に示すようなコントロールボリュームP（および隣接するコントロールボリュームE, W）を考え，両辺を積分する（w < r < e, t < t < t+Δt）：
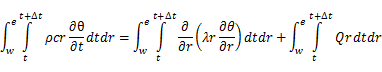......(3)
左辺だけ取り出して積分する。 密度ρと比熱cはw < r < e，t < t < t+Δtでは一定であるとみなすと，
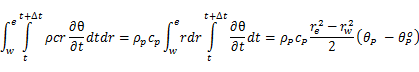......(4)
つぎに右辺第1項だけ取り出して積分する。 温度θはt < t < t+Δtでは一定であるとみなすと，
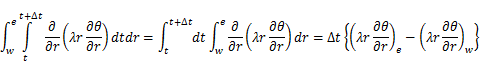......(5)
最後に右辺第2項だけ取り出して積分する。 発熱量Qはw < r < e，t < t < t+Δtでは一定であるとみなすと，
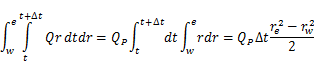......(6)
以上の結果を整理すると式(3)は次のようになる：
......(7)
また陽解法を用いて，
......(8)
......(9)
とする。さらに熱伝導率については調和平均を用いて，
......(10)
......(11)
とする（文献[3]）。
式(7)に式(8)〜(11)を代入すると次の離散化方程式が得られる：
......(12)
この式を図2の格子点と距離の定義を用いて書き直すと，次の式となる：
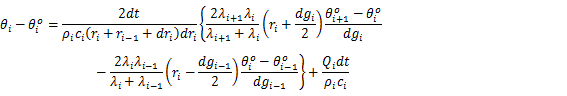......(13)
ここで，to[i]は現在の温度，t[i]は未来（dt時刻後）の温度を表す。
ここで，係数ae[i], aw[i]を次のように定義すると：
......(14)
......(15)
離散化方程式は次のように簡潔に書くことができる：
......(16)
プログラミング用に書き直すと：
となる。
中心軸に位置する格子点1は格子点2との間でしか熱交換をしないので，次の式が成り立つ：
ここで，
である。
保護管表面の熱伝達率をh [W / m^2 K]とすると，表面温度t[ni]と一様流の温度tenvを用いて 保護管表面から一様流への熱流束は次のように表される。
これは保護管内部から保護管表面への熱流束：
と等しいので，次式が成り立つ。
この式を解くと表面温度t[ni]は次式で求められる。
McAdamsは一様流中の円筒周りの平均熱伝達率h [W / m^2 K]を次の式で表している[4]：
ここで，Dは円筒の直径[m]である。今回の問題では保護管の外径0.36[m]をDの値として用いる。
またNuはヌッセルト数であり，次の式で表される。
ここで，レイノルズ数Reが4000〜40000のとき，c1 = 0.174, c2 = 0.618, Re > 40000のとき，c1 = 0.0239, c2 = 0.805である。
またレイノルズ数Reは次の式で表される
つまり，今回の問題の場合，円筒の直径，空気の流速，熱伝導率，動粘性係数がわかれば， 平均熱伝達率hが得られる。ただし，空気の熱伝導率と動粘性係数は温度依存性があるので， 計算を繰り返すたびに，変化する気温に応じて熱伝導率と動粘性係数の値を求め， 新たに求まった平均熱伝達率hを保護管表面の熱伝導・熱伝達計算に使用しなくてはならない。
空気の熱伝導率と動粘性係数の計算のためには「膜温度」と呼ばれる，
円筒表面温度t[ni]と周囲の流体温度tenvの平均値を使用する：
先に，今回の計算では比熱や密度として仮の（適当な）値を与えて非定常計算を行うと述べた。 ここでは計算を単純化するため，ρc = 1.0とする。
しかし，陽解法の計算を安定的に行うためには(1 - ae[i] - aw[i]) がマイナスにならないようにしなくてはいけない。 そのためには，時間刻みdtを十分に小さくする必要がある。 そこで，dt = 10^-7で計算することにする。
必要なパラメータを入力し，計算を実施してみる。
結果は以下の通りである：