|
双曲型熱伝導方程式の導出
解説: 福代和宏 (updated: December 1, 2010)
1. 従来の放物型熱伝導方程式の導出
式(2)を式(1)に代入す ることによって,次式が得られる:
これが従来の放物型熱伝導方程式(Parabolic Heat Conduction Equation)である。
2. フーリエの法則の問題点
しかし実際には,例えば金属内部では伝導電子が移動して熱を伝えるわけであり,温度や熱勾配といった熱の情報が伝わるには時間がかかる。この時間を「分子論的熱緩和時間」という。フーリエの法則は「分子論的熱緩和時間」を無視しているがそれで大丈夫だろうか?一般には(工学的には)大丈夫だとみなされてい る。
3. 双曲型熱伝導方程式へ
これが双曲型熱伝導方程式(Hyperbolic Heat Conduction Equation),通称HHCEである。ここで登場したCとい う変数は温度伝搬速度(speed of heat propagation)も しくは第二音速(speed of second sound)と呼ばれるものであり,ようするに温度情報の伝搬速度である。
では,フーリ エの法則はどうなったかというと,次のように書き換えられた:
ここで文献[6]を参考 に,式(1)と式(6)によって双曲型熱伝導方程式を導出してみる。
まず,式(6)の勾配を求める:
また,式(1)を時間で
偏微分し,
式(1)と式(8)を足すと次式が得られる:
式(9)に式(7)を代入し,
すなわち,
式(10)と式(5)の比較から
4. さらなる改良へ
このようにし て双曲型熱伝導方程式: HHCEなるものが得られたわけだが,これはこれで様々な批判にさらされた。その批判の内容と,AliとZhangによるさらなる改良については稿を改めて紹介する。 −>「相
対論的熱伝導方程式 (Relativistic Heat Conduction Equation)の導出」へ
記号表
参考文献 [1] 川下研介『熱伝導論』(オーム社, 1966年), pp. 44 – 46 [2] P. M. Morse, H. Feshbach, Method of Theoretical Physics, McGraw-Hill, New York, 1953 [3] C. R. Cattaneo: Suruneforme del'équation de la chaleur éliminant le paradoxe d'une propagation instantanée, Compte. Rend. 247 (4) (1958), pp. 431 – 433 [4] P. Vernotte: Les paradoxes de la theorie continue de l'équation de la chaleur, Compte. Rend. 246 (22) (1958), pp. 3154 – 3155 [5] M. Chester: Second sound in solid, Phys. Rev. 131 (15) (1963), pp. 2013 – 2015 [6] Y. M. Ali, L. C. Zhang: Relativistic heat conduction, Int. J. Heat and Mass Transfer, 48 (2005), pp. 2397 – 2406 |
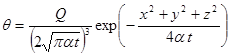 (4)
(4)